大学受験対策で周りと差をつけたい高校生の皆さんに向けて、本記事では筆者が実際に使用していた「数学の受験勉強に使えるウェブサイト」を3つご紹介します。
目次
受験の月
単元ごとにポイントが一目でわかる形にまとめられており、非常にわかりやすいです。説明もかなり詳しく、初心者でも理解しやすいと思います。
思考の進め方も詳しく書かれていて、「なぜその計算をすればいいとわかるのか?」「なぜそのように場合分けすれば良いのか?」といった部分まで理解できるため、簡単には忘れない形で知識を身につけることができます。
ex) 文字を含む2次関数の最大・最小① 区間固定で関数の軸が動く
この記事は、「2次関数の最大・最小問題」解説の第1弾となる記事です。
「何が一定で何が変化するかを常に意識する」「最大・最小は別々に考える」などのポイントが丁寧に説明されているほか、場合分けの基準値を決める方法についても言葉と図で明確に示されており、丸暗記にならないよう工夫されています。
弊教室でも、「グラフを書かずに場合分けを丸暗記した結果、逆向きの2次関数になったり変化する文字が変わったりした途端、対応できなくなる」生徒が多発する単元ですが、この記事を一度読んだ上で練習を積めば、正答率は格段に上がるでしょう。
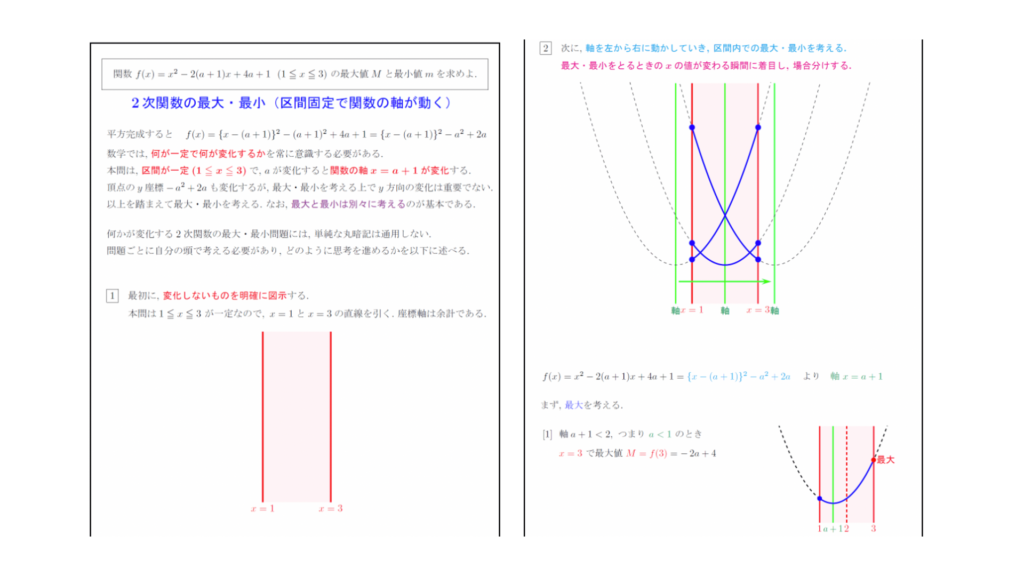
当該記事より、解説部分前半を引用
ex) 確率の極意(何が同様に確からしいか3パターン)
また、大きなくくりで苦手な単元がある場合(「場合の数が苦手」など)、その章の記事を通読することをお勧めします。飛び飛びで読んでも十分効果はありますが、真に効果的な記事は各単元序盤にある総論です。
この記事は、確率の根本的な考え方について述べられたものです。
「(記事冒頭で示された考え方は)多くの教科書や参考書には載っておらず, 学校でも習わないことが多い. しかし, これこそが確率の極意であり, 確率の真の理解のためには避けて通れない. 本項では, 1つの問題に対して複数の考え方での解答を示す. 極論を言えば, 前項と本項の理解で確率の学習が9割方完了する」という文言にも表れている通り、この記事を読むだけで確率の問題の理解度は確実に高まります。

当該記事より、「1から7の数字から異なる4個の数字を選び, 4桁の整数を作る. 奇数である確率を求めよ.」に対する解説部分を引用
高校数学の美しい物語
よく知られた公式・定理の証明や、マニアックな定理・小技の紹介など、ハイレベルな数学の知識を身につけることができます。
数式が見やすく、厳密すぎず省略しすぎない説明でわかりやすさが保証されています。的確かつ良質な例題が各国の数学オリンピックなどから引用されている点も特徴的です。
レベル別に記事を探すこともでき、特に「入試対策の記事」「最難関大学受験対策の記事」が参考になると思います。
ex) 大学受験数学の勉強法(3つのコツ)
この記事は若干特殊で、特定の単元ではなく全単元に通じる話題となっています。
特に「2. ポイントをためる」については私も受験生時代に実践していた方法で、導入することを強くお勧めします。生徒にも「具体的な問題から抽象的なポイントを抽出することが大事」として伝えています。
数学は1問ずつ解法を暗記してもキリがなく、類似した問題に適用できるような法則を見つけることが近道です。これができれば別の科目に勉強時間を回せますが、できない場合は演習量で補填することになり、数学に多大な時間と労力を取られます。
しかし、この作業にも慣れは必要です。自分ではなかなか難しいという場合には、我々医学生講師がポイント抽出のサポートをさせていただきます。

当該記事より、ポイントの例を引用
ex) 漸化式の解き方12パターンと応用例まとめ
このサイトでは「レベル」とは別に「タグ」も使用されており、特に「まとめ」というタグの記事が総ざらいに最適です。レベル分けがされていない記事が多いので、見逃している人も多いかもしれません。
例えば次のような記事があります。
- 因数分解の発展的な公式・応用例まとめ
- 数学的帰納法のパターンまとめ
- 有名な定理を複数の方法で証明
- 数学1の教科書に載っている公式の解説一覧
- 素数にまつわる覚えておくべき性質まとめ
- 大学入試共通テストにも役立つ即効性の高い公式まとめ
中でも漸化式の解き方は多様であり、一巡するだけで適切な使い分けを身につけることは困難です。何らかの形で脳内を整理することが必要で、このサイトのまとめ記事が効果を発揮する好例と言えます。

当該記事より、漸化式の解き方4-6を引用
グラフ計算機 – Desmos
今までとは異なり、グラフを視覚的に確認したい場合に役立つサイトです。
公立の中学校・高校では問題集の解答が配布されない場合も多いですが、このサイトでグラフを描画することで解答を確認することができます。
ただし、空間図形を描きたい場合はGeoGebraという別のサイトを利用しましょう。
ex) 定義域が変化する二次関数の最大値・最小値
二次関数の最大値・最小値を求める問題でx, y以外に文字が登場するとき、場合分けのために図を描くことが推奨されます。Desmosを使えば、aの値によって最大値・最小値が変化していく様子を視覚的に確認することができ、場合分けの基本的な考え方を身につけることができます。
ex) 媒介変数表示で表される曲線
大阪大学の2022年の入試問題で、次の媒介変数表示で表される曲線に関する面積を求める問題が出題されました。
$$x = e^t\,cos\,t + e^\pi,\;y = e^t\,sin\,t\;(\,0≤ t ≤ \pi\,)$$
まず \(x, y\) をそれぞれ \(t\) で微分し増減表を書き、概形を把握することが解答に至る第一歩でした。
これをDesmosで図形に起こすと、次のようになります。
公文式立売堀教室は、大阪市西区で20年以上にわたり地域の教育活動を支えてまいりました。ベテラン講師と医学生講師の協力体制で、幼児から高校生まで幅広い学年の生徒の指導にあたっております。
大学受験を控えた高校生に対しても、京大生・阪大生による添削や質問対応など、実践的なサポートを重ねてまいりました。このサイトでは、大学入試に役立つ情報をお届けしております。
▶︎ 教室の詳細・お問い合わせ・見学申込:こちらからお願いします。




